
.- Optische Täuschungen -.

















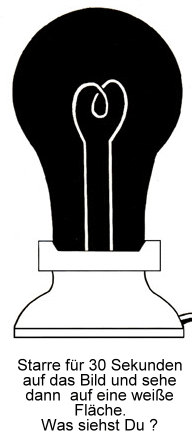
Schau 30sek. lang auf die drei Punkte. Dann schau auf eine weiße Wand und fang an zu blinzeln !





















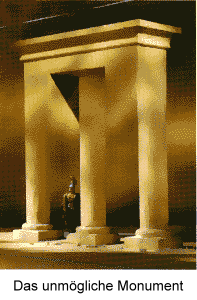






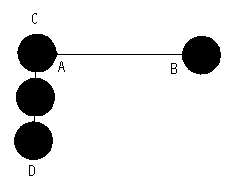
Die Strecke AB scheint größer zu sein als die Strecke CD

Der rechte Bogen scheint kürzer zu sein und eine
größere Krümmung zu haben als der linke.
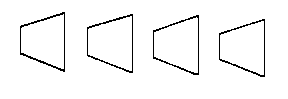
Jede linke Figur scheint größer als jede rechte zu sein, obwohl alle Figuren gleich sind. Die Täuschung verschwindet, wenn man auf die Zeichnung von der rechten Seite so sieht, daß der Blick über die Zeichenfläche gleitet.

Welche Entfernung ist größer AB
oder AC?
Nicht wahr, AC ist größer?
Und jetzt nachmessen!
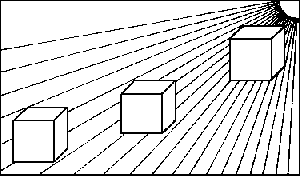
Der rechte Würfel erscheint uns
größer als der linke, obwohl alle drei Würfel gleich sind. Die zusammenlaufenden
Linien nehmen wir als Andeutung der Tiefe des Raumes wahr.

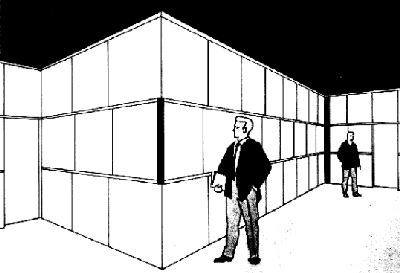
Infolge Nichtbeachtung
perspektivischer Regeln erscheint die Figur des vorangehenden Greises viel höher
als die des Jungen, obwohl die Figuren gleich sind.

Die schraffierte Figur rechts
erscheint jeweils heller als die gleiche Figur auf dem hellen Hintergrund links.

Der linke innere Kreis scheint
größer zu sein
als der rechte innere Kreis.
Die beiden dicken Balken sind in Wirklichkeit gleich lang.
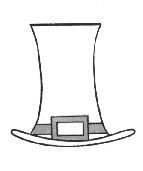
Der Hut ist genauso breit wie hoch.
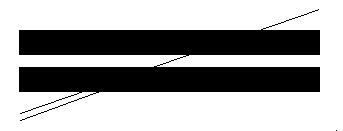
Welche der zwei Linien ist die Fortführung?
Natürlich die obere...
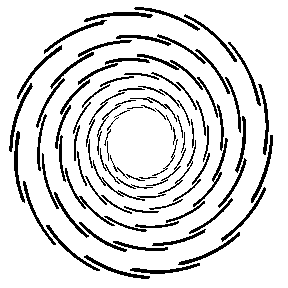
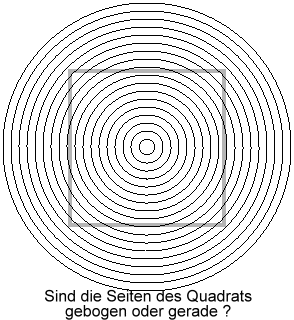
Handelt es sich um eine Spirale, oder einfach nur um Kreise?
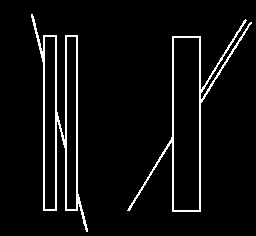
1. Eine Gerade
2. Die obere Linie wird fortgesetzt

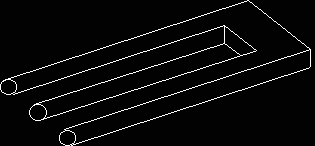
Eine unmögliche Figur.

Der eine Mann geht die Treppe rauf, der andere die Treppe runter - aber beide gehen in die gleiche Richtung.
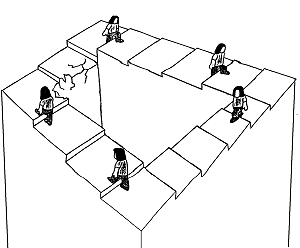
Sie werden wohl nie ankommen...

Wer hat das bloß zusammengebaut?
Dies ist eine Fotografie und wurde so geschickt fotografiert das diese
wundersame Kiste enstand.
Da stellt sich mir doch glatt die Frage, ob man nicht schon leicht verrückt sein
muss um sich sowas ausdenken zu können.

Obwohl das Gebilde wie eine Spirale aussieht, bilden die Teilelemente jeweils geschlossene Kreise.
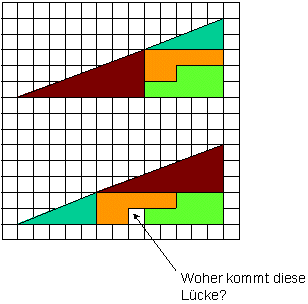
Das große Dreieck ist gar keins,
denn die Hypothenuse hat einen Knick und zwar einmal nach innen und einmal nach
außen, jeweils dort, wo die kleinen Dreiecke aufeinanderstoßen. Das kann man
sehen, wenn man an der Hypothenuse entlangschaut. Etwas analytischer:
Erstmal eine kleine Flächenbetrachtung:
- orangene Flächen: 7 Einheiten
- hellgrüne Flächen: 8 E
- rotes Dreieck: (8x3)/2 = 12 E
- grünes Dreieck: (2x5)/2 = 5 E
macht zusammen: 7+8+12+5 = 32 E
großes Dreieck: (13x5)/2 = 32,5 E
Da kann doch was nicht stimmen...
Da sich die Größen der 4 Flächen tatsächlich nicht ändern, muß wohl die 32,5
falsch sein. Andererseits ist die Flächenberechnung für das große Dreieck
korrekt. Also ist offensichtlich die Annahme falsch, daß die große Fläche ein
Dreieck ist.
Eine mögliche Bestätigung dieser These geht über die Winkel der beiden Dreiecke:
Seien a und b die Winkel unten links des roten resp. grünen Dreiecks. Dann gilt:
- tan(a)=3/8=1/2,66666 und tan(b)=2/5=1/2,5
Also tan(a) ungleich tan(b) und daher a ungleich b.
Wenn aber a ungleich b, dann hat die vermeintliche Hypothenuse den o. g. Knick
und die große Fläche ist kein Dreieck. Die obere Fläche hat 32 E und die unteren
Fläche 33 E.

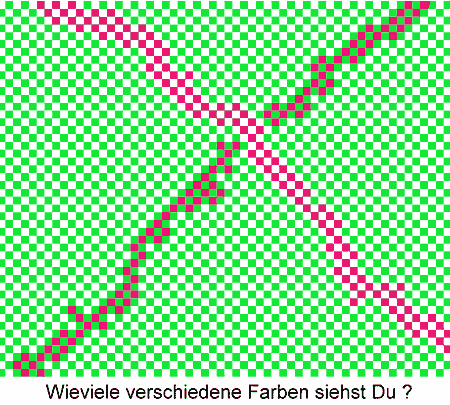
Wie viele verschiedene Farben kann man sehen?
Wie viele Farben sind es aber wirklich?


| Die Wissenschaft hat festgestellt,
dass die Sache mit dem "Schiefen Turm zu Pisa" auf einer optischen Täuschung
beruht.
In Wirklichkeit ist nicht der Turm, sondern alle Häuser um den Turm herum schief. So wie wenn man im fahrenden Zug den Eindruck bekommt, die Landschaft fahre an einem vorüber, genau so bildet man sich ein - wenn man vor den schiefen Häusern und dem geraden Turm steht - es sei der Turm, der schief sei. Dies aber ist eine Täuschung, wie die Wissenschaft festgestellt hat. In Wirklichkeit ist nämlich nicht der Turm ... |
Weitere folgen noch, falls ich noch welche finde !
Diese Seite gehört zu http://ww.KLAB.de ! Solltest du nicht durch diese Url auf diese Seite gekommen sein, dann schreib mir bitte ne E-Mail !
Letzte Update: 01/10/05 17:34:00